Definisi Peracikan
Compounding adalah metode penghitungan suku bunga yaitu bunga efektif atas bunga dimana bunga dihitung atas investasi / pokok awal ditambah bunga yang diperoleh dan investasi kembali lainnya, dengan kata lain bunga yang diperoleh diakumulasi ke jumlah pokok tergantung pada jangka waktu penyetoran atau pinjaman. yang bisa bulanan, triwulanan atau tahunan
Mari kita coba memahami apa itu penggabungan dan cara kerjanya melalui beberapa contoh dasar
4 Contoh Teratas dari Kekuatan Peracikan
Contoh 1
Shane dan Mark memutuskan untuk menginvestasikan $ 1,00,000, tetapi Shane memutuskan untuk berinvestasi dalam bunga sederhana, sedangkan Mark berinvestasi dalam bunga majemuk selama sepuluh tahun dengan bunga 10%. Mari kita lihat apa yang terjadi setelah sepuluh tahun.
Larutan:
Jadi, perhitungan investasi Shane adalah -

Jumlah Pendapatan Total = $ 200.000
Dengan bunga Sederhana, Shane akan mendapatkan $ 2,00,000 setelah 10 tahun.
Perhitungan investasi mark akan -

Jumlah Pendapatan Total = $ 2.59.374
Dengan bunga majemuk, nilai investasi Mark akan tumbuh menjadi $ 2.59.374.
Sekarang Shane memutuskan untuk berinvestasi melalui metode penggabungan seperti Mark, dan mereka berdua menginvestasikan $ 2,00,000 pada tingkat 15%.
Perhitungan investasi Shane akan -

Jumlah Pendapatan Total = $ 8,09,111.55
Shane tetap berinvestasi selama 10 tahun dan mendapatkan jumlah akhir $ 8,09,111,55 dengan tarif 15%.
Perhitungan investasi mark akan -

Jumlah Pendapatan Total = $ 65,83,790.52
Namun, Mark adalah investor jangka panjang yang sabar dan tetap berinvestasi selama 25 tahun, dan nilai investasinya tumbuh menjadi $ 65,83,790.52
Contoh di atas menunjukkan kekuatan peracikan. Semakin panjang horizon investasi, semakin besar pertumbuhan eksponensial.
Contoh # 2 (Mingguan)
Simon memiliki tabungan $ 7500, dan untuk dana kuliah putranya, yang akan melanjutkan ke perguruan tinggi setelah 15 tahun, dia memutuskan untuk berinvestasi di US Savings Bonds. Tujuan Simon adalah menabung $ 20.000, dan tingkat persentase tahunan untuk tabungan obligasi AS adalah 6%. Berapa Nilai Masa Depan Uang Simon setelah 15 tahun?
Larutan:
Diberikan,
- Pokok = $ 7500
- Tarif = 6% atau 0,06
- Jangka Waktu = 15 tahun.
- Berapa kali itu digabungkan dalam satu tahun n = 52 Minggu
- Nilai Masa Depan =?
Jadi, perhitungan nilai masa depan akan -

Rumus untuk penggabungan mingguan adalah sebagai berikut.
F = P (1 + r / n) n * t- F = $ 7500 (1 + 0,06 / 52) 52 * 15
- F = $ 7500 (1 + 0,001153846) 780
- F = $ 18.437,45
Maka dari perhitungan di atas, jelas bahwa tujuan Simon untuk menghemat $ 20,00 tidak akan tercapai dengan cara-cara di atas, tetapi lebih mendekati itu.
Metode Peracikan Berkelanjutan
Sekarang mari kita coba contoh di atas dengan Formula Peracikan Berkelanjutan.
Jadi, perhitungan nilai masa depan akan -

- F = $ 7500e 0,06 * 15
- F = $ 7500e 0,9
- Nilai Masa Depan (F) = $ 18.447,02
Sekarang bahkan dengan Continuous Compounding, tujuan Simon menabung $ 20.000 untuk dana kuliah putranya tidak akan tercapai.
Mari kita lihat dengan Formula Gabungan Bulanan bahwa berapa banyak uang yang perlu diinvestasikan Simon untuk mencapai tujuannya menabung $ 20.000 dalam 15 tahun dengan APR 6%?
Jadi, perhitungan nilai masa depan akan -
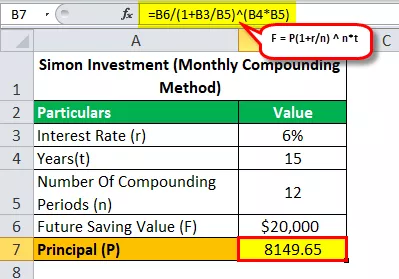
- $ 20.000 = P (1 + 0,06 / 12) 12 * 15
- P = $ 20.000 / (1 + 0,06 / 12) 12 * 15
- Kepala Sekolah (P) = 8149,65
Jadi dengan menyelesaikan persamaan di atas, kita akan mendapatkan jawaban yaitu $ 8.149,65 (Jumlah, yang perlu diinvestasikan Simon untuk mencapai tujuannya menabung $ 20.000 dalam 15 tahun).
Contoh # 3 (Hasil Tahunan Efektif)
Katakanlah bank terbatas XYZ memberikan 10% per tahun kepada warga senior untuk deposito, dan kami berasumsi di sini bahwa bunga bank diperparah secara triwulanan seperti semua bank lainnya. Hitung hasil tahunan efektif selama 5, 7, dan 10 tahun.
Larutan:
Hasil Tahunan selama 5 Tahun:
- t = 5 tahun
- n = 4 (majemuk triwulanan)
- I = 10% per tahun
Jadi A = (1 + 10% / 100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1,6386
- I = 0,6386 dalam 5 Tahun
Bunga Efektif = 0,6386 / 5
Efektif I = 12,772% Per Tahun
Hasil Tahunan selama 7 Tahun:
- t = 7 tahun
- n = 4 (majemuk triwulanan)
- I = 10% per tahun
Jadi A = (1 + 10% / 100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1,9965
- I = 1,9965 dalam 7 Tahun
- Efektif I = 0.9965 / 7
Efektif I = 14,236% Per Tahun
Hasil Tahunan selama 10 Tahun:
- t = 10 tahun
- n = 4 (majemuk triwulanan)
- I = 10% per tahun
Jadi A = (1 + 10% / 100/4) (10 * 4)
- A = (1 + 0,025) 40
- A = 2,685
- I = 1,685 dalam 10 Tahun
- Efektif I = 1.685 / 10
Efektif I = 16,85% Per Tahun
Contoh # 4 - (Annuities: Future Value)
$ 1.000 diinvestasikan setiap 3 bulan pada 4,8% per tahun ditambah kuartalan. Berapa nilai Anuitas dalam 10 tahun?
Larutan:
Jadi ketika kita mengatakan berapa nilai Anuitas dalam 10 tahun berarti di sini kita harus menemukan nilai masa depan, dan ini penting karena setiap kali ada contoh tentang anuitas, kita harus melihat apa yang harus kita temukan.
Jadi rumus Nilai Masa Depan adalah
FV Anuitas = P ((1+ r) n - 1 / r)- P = Pembayaran Berkala
- r = Tarif per periode
- n = Jumlah periode
Jadi rumus Nilai Masa Depan adalah
- Jadi di sini P = $ 1.000
- r = 4,8% Per Tahun atau 0,048
- r (triwulanan) = 0,048 / 4
- r (triwulanan) = 0,012
- n = 10 tahun
- n (Berapa kali penggabungan akan diterapkan) = 10 × 4 = 40
Jadi, perhitungan FV Annuity akan -

Jadi sekarang FV = $ 1000 (1 + 0,012) 40 -1 / 0,012)
Jadi dengan Memecahkan persamaan diatas akan didapatkan FV sebesar $ 50.955,30
Jadi berapa Anuitas dalam 10 tahun dan jawabannya adalah $ 50.955,30
Sebagai tambahan, kita juga dapat mengetahui dari contoh di atas bahwa berapa banyak bunga yang diperoleh dalam 10 tahun.
Karena 40 kali $ 1000 diinvestasikan, itu adalah total investasi (40 × $ 1000 = $ 40.000).
Jadi Bunga = Nilai Masa Depan - Total investasi
- Bunga = $ 50.955,30 - $ 40.000
- Bunga = $ 10.955,30
Jadi di sini, penting untuk dipahami bahwa dalam Anuitas, investor dapat memperoleh banyak bunga. Dalam contoh khusus di atas, setoran sebesar $ 40.000 memberikan, sebagai imbalan, bunga total $ 10.955,30.
Catatan: Anda dapat mengunduh templat Excel yang disediakan di atas untuk perhitungan mendetail.








