Apa Koefisien Korelasi?
Koefisien korelasi digunakan untuk menentukan seberapa kuat hubungan antara dua variabel dan nilainya dapat berkisar antara -1,0 sampai 1,0, dimana -1,0 merupakan korelasi negatif dan +1,0 merupakan hubungan positif. Ini mempertimbangkan pergerakan relatif dalam variabel dan kemudian menentukan apakah ada hubungan di antara mereka.
Rumus Koefisien Korelasi
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Dimana
- r = koefisien korelasi
- n = jumlah observasi
- x = 1 st variabel dalam konteks
- y = 2 nd variabel
Penjelasan
Jika ada korelasi atau dikatakan hubungan antara dua variabel, maka itu menunjukkan jika salah satu variabel berubah nilainya, maka variabel lain juga akan cenderung berubah nilainya, katakanlah secara spesifik yang bisa sama atau sama. arah berlawanan. Bagian pembilang dari persamaan melakukan pengujian dan kekuatan relatif dari variabel yang bergerak bersama, dan bagian penyebut dari persamaan tersebut menskalakan pembilang dengan mengalikan selisih variabel dari variabel kuadrat.
Contoh
Contoh 1
Perhatikan dua variabel berikut, x, dan y, Anda harus menghitung koefisien korelasi.
Di bawah ini diberikan data untuk perhitungan.

Larutan:
Dengan menggunakan persamaan di atas, kita dapat menghitung yang berikut ini

Kami memiliki semua nilai dalam tabel di atas dengan n = 4.
Sekarang mari kita masukkan nilai untuk kalkulasi koefisien korelasi.

Oleh karena itu perhitungannya adalah sebagai berikut:

r = (4 * 25.032.24) - (262.55 * 317.31) / √ ((4 * 20.855.74) - (262.55) 2 ) * ((4 * 30.058.55) - (317.31) 2 )
r = 16.820,21 / 16.831,57
Koefisien akan menjadi -

Koefisien = 0,99932640
Contoh # 2
Negara X adalah negara dengan ekonomi berkembang, dan ingin melakukan analisis independen terhadap keputusan yang diambil oleh bank sentralnya terkait perubahan suku bunga, apakah hal itu berdampak pada inflasi dan apakah bank sentral dapat mengendalikannya.
Berikut ringkasan tingkat suku bunga dan tingkat inflasi yang berlaku di negara secara rata-rata untuk tahun-tahun tersebut diberikan di bawah ini.
Di bawah ini diberikan data untuk perhitungan.

Presiden negara telah mendekati Anda untuk melakukan analisis dan memberikan presentasi tentang hal yang sama pada pertemuan berikutnya. Gunakan korelasi dan tentukan apakah bank sentral telah mencapai tujuannya atau tidak.
Larutan:
Dengan menggunakan rumus yang dibahas di atas, kita dapat menghitung koefisien korelasi. Memperlakukan suku bunga sebagai satu variabel, misalnya x, dan memperlakukan tingkat inflasi sebagai variabel lain sebagai y.

Kami memiliki semua nilai dalam tabel di atas dengan n = 6.
Sekarang mari kita masukkan nilai untuk kalkulasi koefisien korelasi.


r = (6 * 170.91) - (46.35 * 22.24) / √ ((6 * 361.19) - (46.35) 2 ) * ((6 * 82.74) - (22.24) 2 )
r = -5,36 / 5,88
Korelasinya adalah -

Korelasi = -0.92
Analisis: Tampaknya korelasi antara tingkat bunga dan tingkat inflasi adalah negatif, yang tampaknya merupakan hubungan yang benar. Dengan naiknya suku bunga, maka inflasi menurun yang artinya cenderung bergerak berlawanan arah satu sama lain, dan terlihat dari hasil di atas bahwa bank sentral berhasil melaksanakan keputusan terkait kebijakan suku bunga.
Contoh # 3
Laboratorium ABC sedang melakukan penelitian tentang tinggi dan usia dan ingin mengetahui apakah ada hubungan di antara keduanya. Mereka telah mengumpulkan sampel 1000 orang untuk setiap kategori dan mendapatkan tinggi rata-rata dalam kelompok itu.
Di bawah ini diberikan data untuk perhitungan koefisien korelasi.

Anda diminta untuk menghitung koefisien korelasi dan membuat kesimpulan bahwa jika ada hubungan.
Larutan:
Memperlakukan Usia sebagai satu variabel, misalnya x, dan memperlakukan tinggi (dalam cms) sebagai variabel lain sebagai y.

Kami memiliki semua nilai dalam tabel di atas dengan n = 6.
Sekarang mari kita masukkan nilai untuk kalkulasi koefisien korelasi.

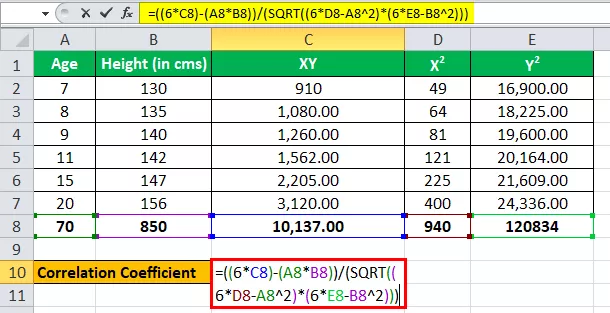
r = (6 * 10,137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20,834) - (850) 2 )
r = 1.322.00 / 1.361.23
Korelasinya adalah -

Korelasi = 0,971177099
Relevansi dan Penggunaan
Ini digunakan dalam statistik terutama untuk menganalisis kekuatan hubungan antara variabel yang sedang dipertimbangkan dan selanjutnya juga mengukur apakah ada hubungan linier antara kumpulan data yang diberikan dan seberapa baik mereka dapat dikaitkan. Salah satu ukuran umum yang digunakan dalam korelasi adalah Koefisien Korelasi Pearson.
Jika suatu variabel berubah nilai dan bersama dengan variabel lain itu berubah nilainya, maka pemahaman bahwa hubungan itu penting karena seseorang dapat menggunakan nilai variabel sebelumnya untuk memprediksi perubahan nilai variabel terakhir. Korelasi memiliki banyak kegunaan ganda hari ini di era modern ini seperti digunakan dalam industri keuangan, penelitian ilmiah, dan di mana tidak. Namun bagaimanapun, penting untuk diketahui bahwa korelasi memiliki tiga tipe hubungan utama. Yang pertama adalah hubungan positif, yang menyatakan jika terjadi perubahan nilai suatu variabel, maka akan terjadi perubahan pada variabel terkait ke arah yang sama. Begitu pula jika terdapat hubungan negatif, maka variabel terkait akan berperilaku berlawanan arah. Juga, jika tidak ada korelasi, maka r akan menyiratkan nilai nol.Lihat gambar di bawah untuk lebih memahami konsepnya.









